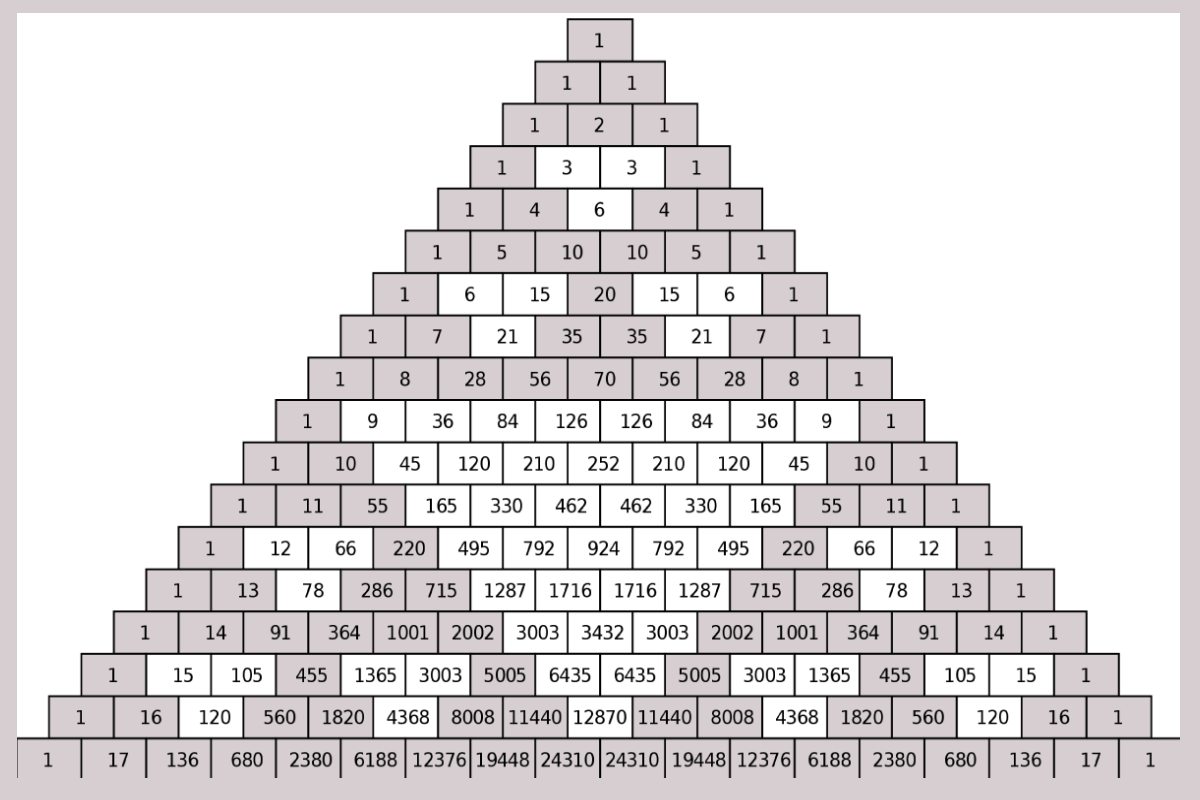
You might have played with the number blocks in your childhood. We used to arrange the numbers of the block in order. Similarly, pascals triangle is also an arrangement of binomial coefficients in a triangular form. The pascal triangle is named after the French mathematician Blaise Pascal thought it was studied by other mathematicians from India, Persia, China, etc long before him. Generally, we use Pascal’s triangle to find the coefficients of binomial expansion, probability of heads and tails in a toss, etc.
Table of Contents
How to Construct the Pascal Triangle?
We start the pascal’s triangle with 1 at the top. As you go downwards the numbers exactly below give you the sum of the numbers above that. Usually, on the sides of the triangle, we get 1. The middle value gives you the sum of the above two numbers. Hence the number of elements in the nth row of the pascal’s triangle is equal to (n + 1) elements.
From the above pascal’s triangle, it is clear that It starts from 1, and the middle elements like 2 is obtained by adding 1 and 1 which are on top of 2. On top of 1, we have only 1 so it continues like that along the sides of the triangle.
Formula to Find the Elements of Pascal’s Triangle:
The pth row and qth column of a pascal triangle can be denoted as
To find the number in the nth row and mth column of Pascal’s triangle we use the Pascal’s triangle formula.
Where n and m are integers such that 0 ≤ m ≤ n.
Example: Find the 4th-row 4th element of the pascal’s triangle.
Solution: We have to find
It means we have to add the 3rd-row 3rd element with the 3rd row 4th element.
Third row 3rd element = 3 and 3rd row 4th element = 1. Hence
Remember the first number 1 is written in the 0th row and 0th column of the triangle.
Pascal’s Triangle in Binomial Expressions
Pascal’s triangle shows the coefficients of the binomial expressions.
Example: (x+1)3 = x3 + 13 + 3x(x+1) = x3 + 3x2 + 3x + 1
- So the coefficients of (x+1)3 are 1, 3, 3, 1.
- If you observe the above pascal triangle, the 3rd row represents the coefficients of (x+1)3. Similarly, the second row shows the coefficients of (x+1)2. Now for (x+y)n, we have (x+y)n = a0xn + a1xn-1y + a2xn-2y2 + … + an-1xyn-1 + anyn
- we can find the value of am using the below formula.
Patterns in Pascal’s Triangle
When you observe the pascal triangle carefully, you can find the following patterns.
- The second diagonal of Pascal’s triangle has the counting numbers.
- Third diagonal of Pascal’s triangle has the triangular numbers and the 4th diagonal has the tetrahedral numbers.
- The triangle is symmetric. The numbers on the right are identical to the numbers on the left.
- The sum of the values of pth rows is 2p. Ex: the sum of the values of the 2nd row is = 1+2+1 = 4 = 22.
- When you add the diagonal elements of the Pascal’s triangle, you get the Fibonacci series.
We can use this Pascal’s triangle in probability to find the number of combinations. Ex: If you toss a coin the probability of getting head and tail is 1. Similarly, if you toss it twice the probability of getting heads is 1, head or tail is 2, and tails are 1. One can learn math topics like Pascal’s triangle in-depth at Cuemath classes. This matches exactly with the 2nd-row elements of Pascal’s triangle. Like this Pascal, the triangle has got many applications for more information about it to log on to the Cuemath website.